

By stating that a vehicle is moving at 60 miles per hour, we are really referring to the rate of motion in relation to the surface the vehicle is traveling on.
Thus, the speed of an airplane is its motion in relation to the air and that of a ship is its motion in relation to the water.
Let’s dig deeper…
In light of the fact that particle motion requires a frame of reference, we will utilize the coordinate axes and four key ideas:
Position determines where a particle or object is located on the x-axis at a given time and is denoted by s(t) or x(t).
Velocity determines how fast the position is changing at time t and gives the direction of movement. Velocity is denoted as v(t) = s’(t)
Acceleration determines how fast the velocity is changing at time t and shows if the velocity increases or decreases. Acceleration is denoted by a(t) = v’(t) = s’’(t)
Velocity is a vector that has magnitude and direction, but speed is a scalar (number) that expresses the absolute speed of an object. Speed indicates how fast an object is moving, but velocity represents speed in a given direction.
Therefore, if s(t) represents the position of a particle along the x-axis at any time t, then the following terms are of importance to our understanding of motion.
Having laid the foundation, let’s move on to learn about particle motion through an example and review some previously learned skills and terms.
Suppose we are given the following position function, measured in meters, \(s(t)=2 t^-2 t^+4\)
What is the object’s initial position?
So, when t = 0, the position of the particle is 4 meters.
Now let’s determine the velocity of the particle by taking the first derivative.
Next, let’s find out when the particle is at rest by taking the velocity function and setting it equal to zero.
Based on our calculations, we find that the particle is at rest at time t = 0 and t = 2/3.
But now, for the interesting question.
During what intervals does the particle move left and right?
Decoding this requires us to search for increasing and decreasing intervals.
Because when the velocity is positive, the particle moves toward the right, and when the velocity is negative, the particle moves toward the left.
Ahh, so we were actually finding critical numbers when we found v(t) = 0. If we test for either positive or negative values on either side of our critical numbers, we will be able to determine when the particle is moving right or left!
Alright, so our number line shows us that since the velocity is positive to the right of t = 2/3, the particle is moving to the right.
And because the velocity is negative between t = 0 and t = 2/3 particle is moving left.
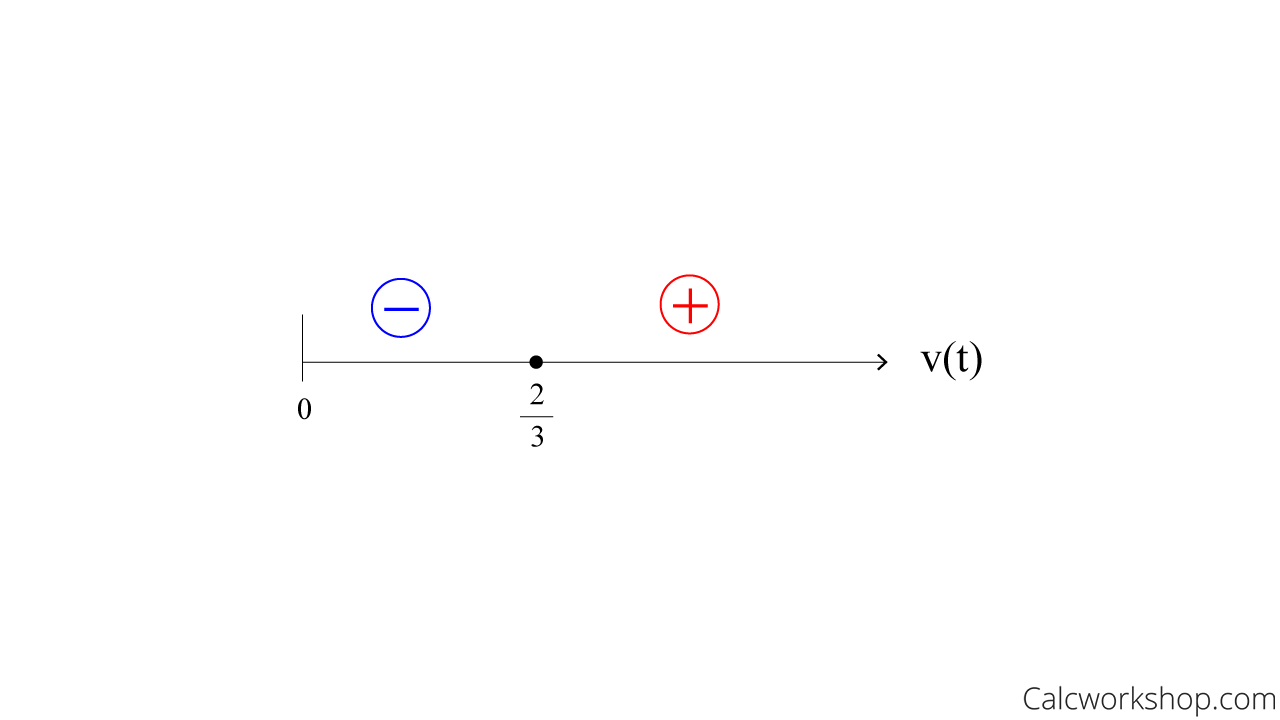
Velocity Number Line

\begin
\begin
\text < Moving Right: >t \in\left(\frac, \infty\right), v(t)>0 \\
\text < Moving Left: >t \in\left(0, \frac\right), v(t)